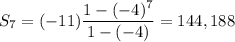For a geometric sequence with common ratio

, we have
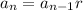
that is, the

-th term in the sequence is the product of the previous term and the common ratio

. So
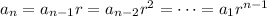
Then the sum of the first 7 terms is
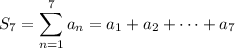
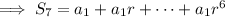
Notice that
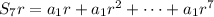
so we can subtract this modified sum from
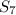
to get
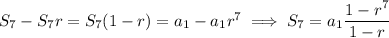
We're told that
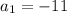
and
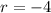
, so the sum of the first 7 terms is