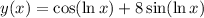Question

Solve the given initial-value problem. x^2y'' + xy' + y = 0, y(1) = 1, y'(1) = 8

Answer 1

Substitute
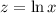
`z=\ln x`, so that


`(\mathrm dy)/(\mathrm dx)=(\mathrm dy)/(\mathrm dz)\cdot(\mathrm dz)/(\mathrm dx)=\frac1x(\mathrm dy)/(\mathrm dz)`


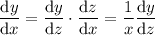
`(\mathrm d^2y)/(\mathrm dx^2)=(\mathrm d)/(\mathrm dx)\left[\frac1x(\mathrm dy)/(\mathrm dz)\right]=-\frac1{x^2}(\mathrm dy)/(\mathrm dz)+\frac1x\left(\frac1x(\mathrm d^2y)/(\mathrm dz^2)\right)=\frac1{x^2}\left((\mathrm d^2y)/(\mathrm dz^2)-(\mathrm dy)/(\mathrm dz)\right)`

Then the ODE becomes



`x^2(\mathrm d^2y)/(\mathrm dx^2)+x(\mathrm dy)/(\mathrm dx)+y=0\implies\left((\mathrm d^2y)/(\mathrm dz^2)-(\mathrm dy)/(\mathrm dz)\right)+(\mathrm dy)/(\mathrm dz)+y=0`

`\implies(\mathrm d^2y)/(\mathrm dz^2)+y=0`

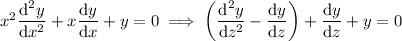
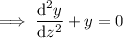
which has the characteristic equation
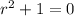
`r^2+1=0` with roots at
`r=\pm i`. This means the characteristic solution for
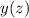
`y(z)` is


`y_C(z)=C_1\cos z+C_2\sin z`

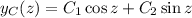
and in terms of
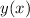
`y(x)`, this is


`y_C(x)=C_1\cos(\ln x)+C_2\sin(\ln x)`

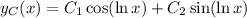
From the given initial conditions, we find


`y(1)=1\implies 1=C_1\cos0+C_2\sin0\implies C_1=1`

`y'(1)=8\implies 8=-C_1\frac{\sin0}1+C_2\frac{\cos0}1\implies C_2=8`

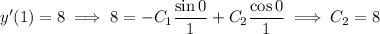
so the particular solution to the IVP is


`y(x)=\cos(\ln x)+8\sin(\ln x)`