Question

Compute the mutual information between x and y where x and y are binary and with joint distribution specified as p(0, 0) = p(0, 1) = p(1, 0) = 1/3.

Answer 1

The mutual information
`MI`


`MI=\displaystyle\sum_(x,y)p(x,y)\ln(p(x,y))/(p(x)p(y))`

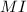
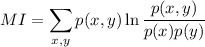
First compute the marginal distributions for
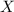
`X` and
`Y`.



`p(x)=\begin{cases}\frac23&\text{for }x=0\\\frac13&\text{for }x=1\end{cases}`


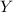
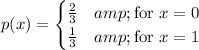
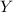
`Y` has the same marginal distribution (replace
`x` with
`y` above).

The support for the joint PMF are the points (0,0), (1,0), and (0,1), so this is what you sum over. We get


`MI=p(0,0)\ln(p(0,0))/(p_X(0)p_Y(0))+p(1,0)\ln(p(1,0))/(p_X(1)p_Y(0))+p(0,1)\ln(p(0,1))/(p_X(0)p_Y(1))`

`MI=\frac13\ln(\frac13)/(\frac23\cdot\frac23)+\frac13\ln(\frac13)/(\frac13\cdot\frac23)+\frac13\ln(\frac13)/(\frac23\cdot\frac13)`

`MI\approx<span>0.174`


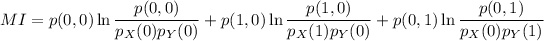
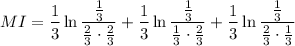
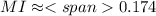
Be sure to check how mutual information is defined in your text/notes. I used the natural logarithm above.