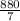Let x represent miles and y represent dollars.
That gives you coordinates (120, 70) and (50, 102.5).
First, find the slope (m) of the line using
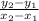
m =
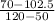
=
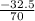
=
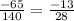
Note: slope is rate of change.
Next, use the Point-Slope formula and solve for y:
y -
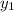
= m (x -
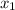
)
y - 70 =
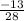
(x - 120)
y - 70 =
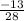
x +
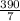
y =
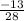
x +
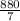 Answer:
Answer: linear function is: y =
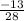
x +
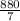
rate of change is:
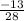
initial value of the function: