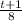Question

How to find (c,d,e)
Please do a step by step working.Thank you.

Answer 1

(a)
The inverse is when you swap the variables and solve for y.
g(t) = 2t - 1 (Note: g(t) represents y)
rewrite as: y = 2t - 1
swap the variables: t = 2y - 1
solve for y: t + 1 = 2y

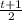
`(t + 1)/(2)` = y
Answer for (a):
`g^(-1)(t)` =
`(t + 1)/(2)`

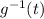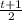
(b)
Same steps as part (a) above:
h(t) = 4t + 3
rewrite as: y = 4t + 3
swap the variables: t = 4y + 3
solve for y:
`y =(t - 3)/(4)`

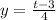Answer for (b):
`h^(-1)(t)` =
`(t - 3)/(4)`

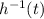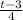
(c)

`g^(-1) ( h^(-1)(t)) = g^(-1) ((t - 3)/(4))`
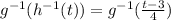
replace all t's in the
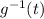
`g^(-1)(t)` equation with
`(t - 3)/(4)`

`g^(-1) ((t - 3)/(4))` =
`( (t-3)/(4) + 1)/(2)`
=
`( (t-3)/(4) + (4)/(4))/(2)` =
`( (t - 3 + 4)/(4))/(2)` =
`( (t + 1)/(4))/(2) = (t + 1)/(8)`
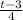
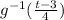
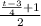
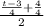
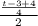
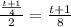Answer for (c):
`g^(-1) ( h^(-1)(t))` =
`(t + 1)/(8)`

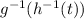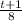
(d)
h(g(t)) = h(2t - 1) = 4(2t - 1) + 3 = 8t - 4 + 3 = 8t - 1
Answer for (d): h(g(t)) = 8t - 1

(e)
h(g(t)) = 8t - 1
y = 8 t - 1
t = 8y - 1
t + 1 = 8y

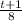
`(t + 1)/(8)` = y
Answer for (e): inverse of h(g(t)) =
`(t + 1)/(8)`