Question

Find sin 105 degrees by using 105 degrees = 60 degrees + 45 degrees

Answer 1

This is the rule of sums of trig identities. It says that sin(a + b) = sina*cosb+sinb*cosa. Set up your right triangles. In a 30-60-90 triangle, the side across from the 60 angle is the square root of 3, the side across from the 30 is 1, and the hypotenuse is 2. In a 45-45-90 the sides across from the 45 degree angles are 1 and the hypotenuse is square root of 2. With that being said, the sin of 60 is
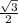
`( √(3) )/(2)` and the cos of 60 is 1/2. Both the sin and cos of 45 is
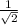
`(1)/( √(2) )`. So your formula is filled in like this:
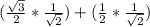
`( ( √(3) )/(2) * (1)/( √(2) ))+( (1)/(2) * (1)/( √(2) ))`. When you do the multiplication on those sets of parenthesis, you get
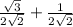
`( √(3) )/(2 √(2) ) + (1)/(2 √(2) )`. When you add those your solution is
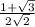
`(1+ √(3) )/(2 √(2) )`. Depending upon your instructor you may have to rationalize that denominator to get that radical out from under there, but if not, that's pretty much it!