Question

Select all the correct locations on the table.

Answer 1

The desired average rate of change is -60.

Consider the first and the last point of the table.

These points are (1, 27) and (5, -213)

The rate of change of a function is given as:


`(f( x_(2) )-f( x_(1) ))/( x_(2) - x_(1) )`

x₂ is the last point and x₁ is the first point. Using the values we get:


`(-213-27)/(5-1) \\ \\ = (-240)/(4) \\ \\ =-60`

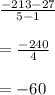This means, the first and the last point give an average rate of change of -60.

Answer 2

Be
`y=f(x)`, a rate of change is defined by the following equation:


`(\Delta y)/(\Delta x)=(y_(2)-y_(1))/(x_(2)-x_(1))`

So, the problem establishes that we need to find out two points with an average rate of -60. So, the table above shows five points. Hence, we will take two of them, say:


`P_(1)(1, 27)`

`P_(2)(5, -213)`

Therefore:


`(\Delta y)/(\Delta x)=(-213-27)/(5-1)=\boxed{-60}`

So these two points are the ones we were looking for.