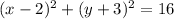Question

Write the equation of the circle with Center (2, -3) and a radius of 4

Answer 1

(x-a)^2 + (y+b)^2 =r^2 where (a,-b) is the center and r is the radius.

check: (x-2)^2+(y+3)^2 == (2,-3)
r^2=16 == sqrt(16) =4

Answer 2

`(x-2)^(2) + (y +3)^2 = 16`

Explanation:

The general form of equation of a circle is
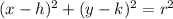`(x -h)^(2) + (y -k)^(2) = r^2`, where (h, k) is the center and r is the radius of the circle.

We are going to use the form to find the equation of a circle.

Given: Center = (h, k) = (2, -3) and radius(r) = 4

Now plug in these given values in the above form, we get

`(x -2)^(2)  + (y - (-3))^2 = 4^2`

Now we can simplify the above equation.

-(-3) = + 3 and 4^2 = 4*4 = 16

So, we get
`(x -2)^(2) + (y +3)^2 = 16`