Question

We are interested in the dimensions of a certain square. A rectangle has length triple the sides of this square and width two units less than the side of this square. Which equation describes this situation if the two areas are equal?

Answer 1

To answer this question, let's first understand what we are dealing with. We have a square and a rectangle, and we know two things:

1. The side length of our square is denoted as "s".
2. The length of our rectangle is triple the side length of the square ("3s"). The width of our rectangle is two units less than the side of the square ("s - 2").

Now we need to form an equation based on the information that the areas of the square and the rectangle are equal.

The area of a square is calculated by squaring its side, so the area of our square is "s * s" or "s^2".

The area of a rectangle is calculated by multiplying its length by its width, so the area of our rectangle is "3s * (s - 2)".

We are told that the areas of the square and the rectangle are equal, so we can set our two area equations equal to each other:

s^2 = 3s * (s - 2)

And there you have it, that is our equation which describes the situation.

Answer 2

If we assume that the length of the sides of the square are x, then the resulting area will then be:


`A=l*w=x*x= x^(2)`

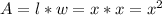
Then we have the rectangle, whose length triples the square. This will be represented by: 3x

And the width of this rectangle is 2 units less than the side of the square, so it is represented as: (x - 2)

The area of the rectangle can then be represented by:


`A=l*w=3x(x-2)`

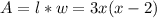
The questions says that the two areas are equal, so set the areas equal to each other, and you get:


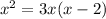`x^(2) =3x(x-2)` or C