Suppose we choose

and
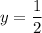
. Then
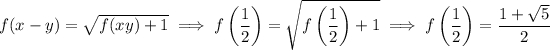
Now suppose we choose
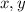
such that
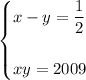
where we pick the solution for this system such that
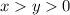
. Then we find
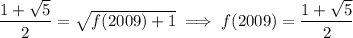
Note that you can always find a solution to the system above that satisfies
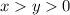
as long as
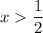
. What this means is that you can always find the value of

as a (constant) function of
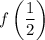
.