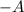Question

1. The height of a soccer ball that is kicked from the ground can be approximated by the function:

y= -18x^2 + 90x
where y is the height of the soccer ball is x seconds after it is kicked.
Find the time, in seconds, it takes from the moment the soccer ball is kicked until it returns to the ground.

2. The height of a soccer ball that is kicked from the ground can be approximated by the function:
y = -16x^2 + 64x
where y is the height of the soccer ball in feet x seconds after it is kicked. What is the soccer ball's maximum height in feet?

Answer 1

2.
`\displaystyle 64\:feet`

1.
`\displaystyle 5\:seconds`

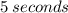
Explanation:

2. Sinse we do not have a y-intercept [C-value in this case], we have to use a part of the quadratic formula to solve for x, and rewrite this equation in Vertex Form, with
`\displaystyle [h, k]` as the vertex point. Observe:

`\displaystyle -(b)/(2a) = x \\ \\ -(64)/(2[-16]) = (-64)/(-32) = 2`

Now, keep in mind that
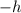`\displaystyle -h` in the vertex formula,
`\displaystyle y = a[x - h]^2 + k,` gives you the OPPOSITE TERMS OF WHAT THEY REALLY ARE, so in this case, sinse 2 is already positive, you do not need to alter its operation sign. With this being stated, you should already have this:

`\displaystyle y = -16[x - 2]^2`

Now, to find k, all you have to do is plug 2 into the TOP equation to get your maximum height:

`\displaystyle -16[2]^2 + 64[2] = -16[4] + 128 = -64 + 128 = 64 \\ \\ \\ y = -16[x - 2]^2 + 64`

Therefore, sinse 64 is your k-value, 64 feet is indeed your maximum height.

1. Simply factour the quadratic equation:

`\displaystyle y = -18x^2 + 90x \\ 0 = -18x[x - 5] \\ \\ 5, 0 = x`

In this case, from a height of sixty-four feet, it is IMPOSSIBLE for the football to hit the ground in zero seconds, therefore the ball will reach the ground in 5 seconds, which makes alot more sence.

I am joyous to assist you at any time.

** Minimum Height →
`\displaystyle A`

** Maximum Height →
`\displaystyle -A`