Answer:
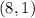
Explanation:
We have been given a system of linear equations:
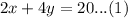
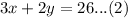
We will use substitution method to solve linear equation. From equation (1) we will get,
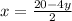
Substituting this value in equation (2) we will get,
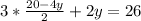
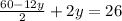
Let us have a common denominator.
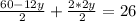
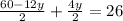
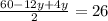
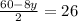
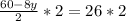
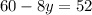
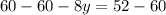
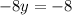
Upon dividing both sides by
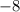 we will get,
we will get,
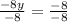
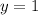
Upon substituting
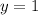 in equation (1) we will get,
in equation (1) we will get,

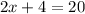
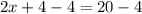
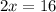
Upon dividing both sides of the equation by 2 we will get,
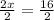
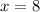
Therefore, the solution of our given system of equations is
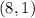 .
.