Question

10 POINTS!!! FULL ANSWER IN STEP BY STEP FORMAT!!

Answer 1

Remark
This question likely should be done before the other one. What you are trying to do is give C a value. So you need to remember that C is always part of an indefinite integral.

y =
`\int (cos(x) + sin(x) ) \, dx = \int{cos(x) \,dx + \int sin(x) \,dx`
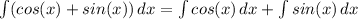
y = sin(x) - cos(x) + C
y(π) = sin(π) - cos(π) + C = 0
y(π) = 0 -(-1) + C = 0
y(π) = 1 + C = 0
C = - 1

y = sin(x) - cos(x) - 1 <<<<< Answer

Problem Two
Remember that
`y = \int\ { (1)/(x) } \, dx = ln(|x|) + C`
y( - e^3 ) = ln(|x|) + C = 0
y(-e^3) = ln(|-e^3|) + C = 0
y(-e^3) = 3 + C = 0
3 + C = 0
C = - 3

y = ln(|x|) - 3 <<<< Answer