Answer:
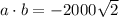
Explanation:
Given information: |a| = 80, |b| = 50, the angle between a and b is 3π/4.
We need to find the dot product a · b.
The formula of dot product is
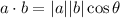
where, θ is the angle between a and b.
Substitute the given values in the above formula.
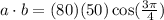
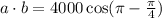
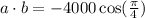
![[\because \cos (\pi-\theta)=-\cos \theta]](https://img.qammunity.org/2019/formulas/mathematics/college/miskxasjr7x0t5fs7u3o8egr9iuhcsn415.png)

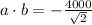
Rationalize the above equation.


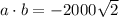
Therefore, the value of a · b is
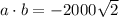 .
.