A normal distribution of data has a mean of 90 and a standard deviation of 18. what is the approximate z-score for the value 64? –3.6 –1.4 1.4 3.6

Question

asked May 18, 2019 166k views

2 Answers

Emre Erkan · Answer 1 · 2019-05-22T22:45:11+0000

Answer:

The approximate z-score for the value 64 is -1.4.

Explanation:

Since, the z-score or standard score for the value x is,

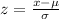
$z=(x-\mu)/(\sigma)$

Where,

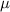$\mu$ is the mean score,

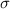$\sigma$ is the standard deviation,

Here, x = 64,

$\mu=90$

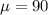
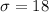
$\sigma=18$

Hence, the z-score for the value 64 is,

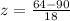
z=(64-90)/(18)

=(-26)/(18)

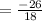
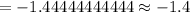
$=-1.44444444444\approx -1.4$

Second option is correct.