Question

Given: KLMN is a trapezoid m∠K = 90°, m∠N = 45° LK = LM = 10 Find: KN, Area of KLMN

Answer 1

Let KLMN be a trapezoid (see added picture). From the point M put down the trapezoid height MP, then quadrilateral KLMP is square and KP=MP=10.
A triangle MPN is right and isosceles, because
m∠N=45^{0}, m∠P=90^{0}, so m∠M=180^{0}-45^{0}-90^{0}=45^{0}.Then PN=MP=10.
The ttapezoid side KN consists of two parts KP and PN, each of them is equal to 10, then KN=20 units.
Area of KLMN is egual to
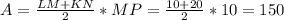`A= (LM+KN)/(2) *MP= (10+20)/(2) *10=150` sq. units.