First, lets determine

(the number of elements in
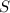
).
We can see that the negative even integers that are between -27 and 0 are: -24, -22, -20, -18, -16, -14, -12, -10, -8, -6, -4, and -2.
This means

.
A proper subset of
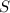
is can't be
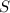
itself, this means the a proper subset of
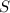
can't have 13 elements.
Given that re-arranging the elements of any set doesn't yield a different set, we use combinations (binomial coefficients) to get the number of subsets in a particular set.
The number of subsets of
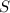
with 1 element are given by
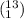
(which means 13 combine 1), in the same way the number of subsets with 2 elements is given by
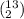
and so forth until reaching the number of subsets with 12 elements.
The previous statement can be written as:

In the previous summation we also included the empty subset, which is always a proper subset of
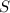
.
So

is an acceptable answer, but we can simplify it.
The following statement is true (it can be easily proven):
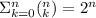
From our previous discussion, this means that the number of subsets of any arbitrary set
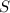
is equal to
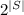
.
This means that the number of proper subsets (which is the number of subset minus the set itself, for finite subsets) is equal to
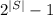
.
So, the answer is:
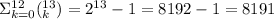 There are 8191 proper subsets of
There are 8191 proper subsets of
 .
.