Question

The sum of two integers is 74. The larger is 26 more than twice the smaller.Find the two integers

Answer 1

Let... the smaller integer be x

Then, the larger integer is 2x+26(Two times.. =2x, 26 more... is =2x+26

Both added is 74

2x+26=74

2x=74−26

2x=48

x=24

Answer 2

Let two integers be x and y.

Consider x > y

The sum of two integers is 74.

⇒ x+y = 74 .....[1]

It is also given that: The larger is 26 more than twice the smaller

⇒x = 2y +26 ......[2]

Substitute equation [2] into [1] we have;

`2y+26+y = 74`

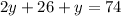
Combine like terms;

`3y+26= 74`

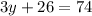
Subtract 26 from both sides we have;

3y = 48

Divide both sides by 3 we have;

y = 16

Substitute the value of y in [2] we have;

x = 2(16)+26 = 32+26

x = 58

Therefore, the two integers are 58 and 16