I'll assume
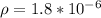
(resistivity of the wire), I'm pretty sure this is the case given that the units you provided go accordingly with those of resistivity.
For a wire with cross-sectional area
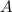
, length
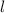
, and resistivity
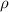
, then its resistance
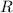
is given by:
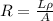
So, for your example:
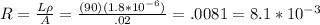 Hence, the answer is C.
Hence, the answer is C.