Question

The center of a hyperbola is located at (0, 0). One focus is located at (0, 5) and its associated directrix is represented by the line y = 9/5 . Given the standard form of the equation of a hyperbola, what are the values of a and B

y^2/a^2 + x^2/b^2 = 1
A=
B=

Answer 1

a=3, b=4

Explanation:

Answer 2

For a hyperbola
`(y^(2))/(a^(2))-(x^(2))/(b^(2))=1`
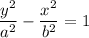
where
`a^(2)+b^(2)=c^(2)`
the directrix is the line
`y=(a^(2))/(c)`
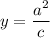
and the focus is at (0, c).

Here, we have c = 5, a² = 9, so b² = 5² - 9 = 16.
a = √9 = 3
b = √16 = 4

Your hyperbola's constants are ...
a = 3
b = 4


______
Please note that the equation of a hyperbola has a negative sign for one of the terms. The equation given in your problem statement is that of an ellipse.