Answer:
Option: a is the correct answer.
a. f(x)
Explanation:
- We are given a set of values for the function f(x) as:
x y =f(x)
0 −5
1 0
2 3
3 4
4 3
5 0
6 −5
Clearly from the set of values we could observe that:
The maximum value of the function f(x) is: 4
- Now we are given function g(x) as:

We know that maximum value of g(x) is attained when the cosine function attains the maximum value.
Also the maximum value of cosine function is: 1
Hence, the maximum value of g(x) is : 4-2=2
- Now we are given a quadratic function h(x) as:
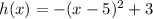
As we know that the function:
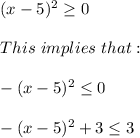
Hence, the maximum value of function h(x) is: 3
Hence, the function that has the largest maximum is:
f(x) ( which is 4)