Hey there! :)
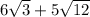
In order to add these together, we must simplify the square roots.
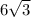
is already in simplest terms, but
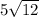
is not.
So, let's start simplifying it!
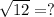
We need to take out any squares within 12.
So, if we branch out 12, we know that 4 × 3 = 12
√4 = 2. So, we can take out 2 and be left with √3.
Since the original square is 5√12, we MUST multiply 5 by 2.

So, using the simplified number of 5 root 12, we now can add this to 6 root 3.
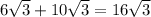
So, our final answer is :
~Hope I helped!~