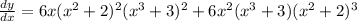We're given the following equation:
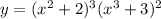
In order to find

we must differentiate both sides of the equation.
Lets start differentiating the left side (

):

The

simply servers to let us know we're differentiating whatever follows it (in this case

) with respect to

.
What we used to get the result is called the "power rule for differentiation" it states the following:
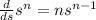
In which

is any variable (in the previous case

) and

is any constant (in the previous case this
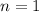
).
Now we'll differentiate the right side of the equation (
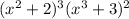
):
![(d)/(dx)(x^2+2)^3(x^3+3)^2=[6x(x^2+2)^2(x^3+3)^2+6x^2(x^3+3)(x^2+2)^3]dx](https://img.qammunity.org/2019/formulas/mathematics/college/gokjigk8hlp9iqk770t7eogm57osyymq36.png)
What we did to differentiate the right side was, first, apply something called "product rule" for differentiation, it states the following:
![(d)/(ds)[f(s)g(s)]= (d)/(ds)[f(s)]g(s)+(d)/(ds)[g(s)]f(s)](https://img.qammunity.org/2019/formulas/mathematics/college/uluapyujye159tlmve0lwo9xua09xxdidl.png)
In which
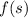
and

are arbitrary functions of an arbitrary variable (

) (in this case
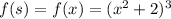
and
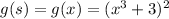
).
After that we applied something called "chain rule" for differentiation, which states the following:
if
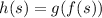
, then
![(d)/(ds)[h(s)]= (d)/(ds)[g(f(s))] (d)/(ds)[f(s)]](https://img.qammunity.org/2019/formulas/mathematics/college/jae5vwkz001u1q24cppze21eidf1hj70c6.png)
Finally, the
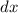
we introduced as a factor after differentiating the right side (we also did it with the left side but with a

) is a consequence of the chain rule, it is always done.
Finally, equaling both differentiated sides of the equation we have:
![dy=[6x(x^2+2)^2(x^3+3)^2+6x^2(x^3+3)(x^2+2)^3]dx](https://img.qammunity.org/2019/formulas/mathematics/college/42vqf919k5ype4kcw8yz44xoawcz8yms0d.png) We solve for
We solve for
 , and the answer is:
, and the answer is: