Question

1. y = –x2 – 1

Reflected across the x-axis
2. y = –(x – 1)2 – 1
Translated left by 1 unit
3. y = x2 + 1
Reflected across the y-axis
4. y = –x2
Translated down by 1 unit
5. y = –(x + 1)2 – 1
Translated right by 1 unit
6. y = –x2 – 2
Translated up by 1 unit


which one goes to which?

Answer 1

Hello, I will just explain the following items with respect to the base equation
`y=x^(2)` since each item performs one or more translations and reflections among the given choices.

ITEM #1: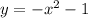
`y=- x^(2) -1`
For this item we have the negative sign added to
`x^(2)` and the added term
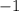
`-1`. The negative sign would indicate that all y values would be multiplied by negative one thus we can expect the graph to be reflected across the x-axis.

Meanwhile, the added term
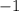
`-1` would tell us that all y values would be 1 lesser than the original. Thus the graph would be translated down by 1 unit.

ITEM #2:
`y=-(x-1)^(2) -1`
For this translation we can still see the negative sign and the added term in the previous item thus we know that this graph is also reflected across the x-axis and translated down by 1 unit.

The only new change for this one is the -1 that is added inside the squared term. We can examine this by comparing
`y=x^(2)` and
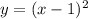
`y=(x-1)^(2)`. Notice that y would be zero in the second equation only when the x value is 1, as opposed to when the x value was zero in the previous equation. This will lead us to conclude that the graph will also be translated right by 1 unit.

ITEM #3: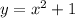
`y=x^(2)+1`
Here we only have the added term
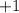
`+1` at the end of the equation. The translation here will work the same as when the added term was
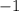
`-1` with the only difference that, instead of translating the graph downward, we will have to translate it upward by 1 unit.

ITEM #4: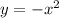
`y=-x^(2)`
For this item we only have the negative sign added to the equation. We have already covered it in the previous items and the reflection will basically work the same for this one. The graph will also be reflected across the x-axis.

ITEM #5: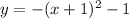
`y=-(x+1)^(2)-1`
Here we can see three changes to the original equation. We have already covered the negative sign before the squared term and the added term -1 so we know that the graph will be reflected across the x-axis and translated down by 1 unit.

For the added 1 inside the squared term, the same rule for the one in item #2 follows only that this time it will be the other way around. The graph will be translated left by 1 unit.

ITEM #6: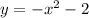
`y=-x^(2)-2`
Lastly, for this one, we only have the negative sign and the term -2 added to the equation. We have already tackled the negative sign so we know that the graph will be reflected across the x-axis.

For the added term, it will work the same as -1 but instead it will just be translated downward by 2 units.