Question

A stone is dropped from the edge of the roof. (A) how long does it take to fall 4.9m

Answer 1

Since the stone is being dropped, you know that it is in free fall. That means you can use your kinematics equations, since acceleration is free fall is a constant 9.8 m/s^2 down.

Looking through the kinematics equations, you want to use one that lets you find t, time, while using variables that we already know the values of. Notice that in the equation:

`x_f = x_(0) + v_0 t + (1)/(2) a t^2`

Say that the rock starts at point x=0. That means the initial value of x, the position, is
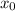
`x_0` = 0m, and the final position is
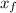
`x_f` = -4.9m. We are also told that the initial velocity,
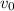
`v_0` = 0, assuming it's being dropped from rest, and a = -9.8 m/s^2. Plug these numbers in and solve for t:

`x_f = x_0 + v_0 t + (1)/(2) a t^2\\ x_f - x_0 = (1)/(2) a t^2\\ -4.9 - 0 = (1)/(2) a t^2\\ -9.8 = a t^2\\ -9.8 = -9.8 t^2\\ 1 = t^2\\ t = 1 \: second`

-----

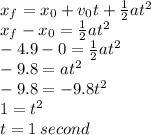
Answer: t = 1 s