Question

there are 10 students in a social studies class. three students will be selected to present their term projects today. in how many different orders can three students be selected? OPTIONS : 120,720,60,1440

Answer 1

The answer is equivalent to 10*9*8 as their is one less student to go after each presentation.
720 ways.

Answer 2

The number of ways this can be done is:

720

Explanation:

Total number of students are: 10

Now out of these 10 students we are asked to select 3 students.

We know that when we have to choose r items and also the order matters out of a total of 10 items the number of ways of doing so is calculated by the method of per as:

`n_C_r=(n!)/((n-r)!)`

Here we have:

n=10 and r=3

Hence, the number of ways of doing so is calculated as:

`{10}_C_3=(10!)/((10-3)!)\\\\\\{10}_C_3=(10!)/(7!)\\\\\\{10}_C_3=(10* 9* 8* 7!)/(7!)\\\\\\{10}_C_3=10* 9* 8\\\\{10}_C_3=720`

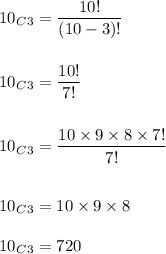
Hence, the answer is:

720