Question

You invest $4000 in a bank account with 5% interest compounded annually. You are wondering how long it would take for your money to double

Answer 1

a

Explanation:

edge 2021

Answer 2

The formula for compound interest is written as
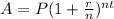
`A = P(1 + (r)/(n))^(nt)`, where P is the principal (initial amount), r is the rate of interest, n is the number of times it's compounded per year, and t is the time in years. With the values from this problem plugged in, it looks like:


`A = 4000(1.05})^(t)`

Since you're trying to find when your money will double, put 8000 for A and solve for t :


`8000 = 4000(1.05})^(t) \\ \\ 2 = (1.05})^(t) \\ \\ t=log_(1.05)2 \\ \\ t = 14.20669908289`

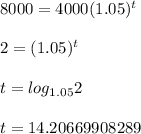
It will take approximately 14.21 years, or about 14 years, 2 months, and 16 days, for the money to double.