Question

Given that a function, g, has a domain of -20 ≤ x ≤ 5 and a range of -5 ≤ g(x) ≤ 45 and that g(0) = -2 and g(-9) = 6, select the statement that could be true for g.

A) g(-4)=-11
B) g(-13)=20
C) g(0)=2
D)g(7)=-1

Answer 1

The answer is B

Explanation:

Answer 2

The correct answer is B.
Here is why each of the remaining answers is not correct. That is, why they cannot be true for g.
AThe function g has a range between -5 and 45 inclusive. That is
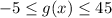
`-5 \leq g(x) \leq 45`. Here you are told that g(-4)=-11 but this can't be as -11 is not in the range. It is not between -5 and 45.
CYou were told in the problem that g(0)=-2. This answer choice suggests that g(0)=2. Since you are told that g is a function, it must be the case that every element in the domain (every x) is paired with at most one element in the range (g(x)). So, it cannot be the case that 0 is paired with both -2 and 2. If it were true then g would not be a function and you were told that it is.
DThe domain of the function (all possible values of x) is given as
`-20 \leq x \leq 5`. Here you are told that g(7)=-1. This cannot be true because 7 is not in the domain which means that the function g is not defined there.