Question

Gina coaches a tennis team. She has 10 tennis balls remaining for practices and needs to purchase more tennis balls for the team. Gina usually tries to have around 150 to 200 tennis balls available for her team to practice with. She is considering purchasing tennis balls which come in canisters that each contain 3 tennis balls.

Function f represents the total number of tennis balls she will have after purchasing c canisters.

A reasonable domain for function f is _≤ c ≤_ .


A reasonable range for function f is _≤ f(c) ≤_ .

Answer 1

Gina has 10 tennis balls and she needs to have between 150 and 200. If we subtract 10 from these values we see that she needs to buy between 140 and 190 tennis balls. As the balls come in canisters of 3 she needs to buy between (140/3) and (190/3) canisters.
The thing to keep in mind, since 140/3 and 190/3 do not give a whole number answers is that Gina can't fall below buying 140 or above buying 190 balls. When you keep that in mind you she needs to buy no less than 47 canisters and no more than 63.
Why? 47 canisters with 3 balls in each give: 47(3)=141 balls and 63(3) = 189 balls.
f is the function that represents all the tennis balls she has and c is the number of canisters.
A reasonable domain is
`47 \leq c \leq 63` since the number of canisters she buys can be anything between 47 and 63 inclusive.
Now if she buys 47 canisters she ends up with (47)(3)+10 = 151 balls all together and if she buys 63 she ends up with (63)(3)+10 = 199 balls all together. So the domain is
`151 \leq f(c) \leq 199`
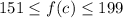
I am surprised you were not asked to generate the function. Here you would have
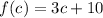
`f(c)=3c+10` with the domain restricted to the values we gave earlier.