Question

1. The equation of a parabola is given.

y = 1/8x^2 + 4x + 20
What are the coordinates of the focus of the parabola?

2. The equation of a parabola is (y - 1)^2 = 16(x + 3).
What is the equation of the directrix of the parabola?

Answer 1

Question 1)

The given parabola is:


`y= (1)/(8) x^(2) +4x+20`

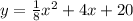
First we need to convert this equation to the general form similar to:


`4p(y-k)=(x-h)^(2)`

So, the given equation will be:


`y= (1)/(8) x^(2) +4x+20 \\ \\ y= (1)/(8)( x^(2) +32x)+20 \\ \\ y= (1)/(8)( x^(2) +32x+256)+20- (1)/(8)(256) \\ \\ y = (1)/(8)(x+16)^(2)-12 \\ \\ y+12= (1)/(8)(x+16)^(2) \\ \\ 8(y+12)=(x+16)^(2) \\ \\ 4*2(y-(-12))=(x-(-16))^(2)`

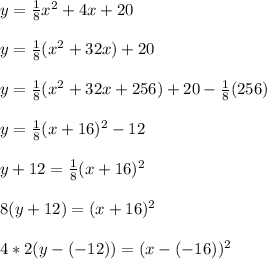
Comparing given equation with the general equation, we can write:
p = 2
h = -12
k= -16

The focus of the parabola with squared x terms lies at (h , k+p)
Using the values, we get the focus point of the given parabola (-16, -10)

Question 2.

The equation of the parabola is:

`(y-1)^(2)=16(x+3) \\ \\ (y-1)^(2)=4*4(x+3)`

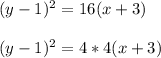
This means:
p=4
h = -3
k =1

The directrix of the parabola with squared y term has the equation of the form:

x = h - p

Using the values, we get

x= - 3 - 4 = -7

So, the equation of the directrix of the parabola will be x = -7