Question

A country's population in 1995 was 228 million. In 2001 it was 230 million. Estimate the population in 2010

Answer 1

every 6 years it goes up by 2 million, so in 9 years it would go up by 3 million. in 2010 it will be 233 million.

Answer 2

The population would be 233 million ( approx )

Explanation:

Let the function that shows the population ( in millions ) after x years,

`f(x)=ab^x`

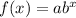
Suppose the population is estimated from 1995,

That is, for 1995,

x = 0,

Given, y = 228 for 1995,

`228=ab^0\implies a = 228`

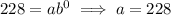
Now, years from 1995 to 2001 = 6,

For x = 6, y = 230,

`230=ab^6`

`230=228(b)^6`

`\implies b =1.00145667325\approx 1.00146`

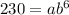
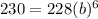
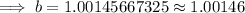
Hence, the equation that shows the given scenario is,

`y=228(1.00146)^x`

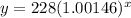
If x = 15,

`y=228(1.00146)^(15)=233.044554776\approx 233`

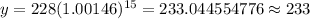
Hence, the estimated population in 2010 would be 233.