Question

Law of sines: How many distinct triangles can be formed for which m∠A = 75°, a = 2, and b = 3?

Answer 1

According to the law of sines:


`(a)/(sin(A)) = (b)/(sin(B))`

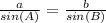
Using the given values, we can find the angle B and find the number of possible triangles that can be formed.


`(2)/(sin(75))= (3)/(sin(B)) \\ \\ sin(B)=3* (sin75)/(2) \\ \\ sin(B)=1.45 \\ \\ B=sin^(-1) (1.45)`

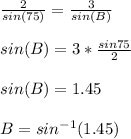
The range of sin is from -1 to 1. The above expression does not yield any possible value of B, as sin of no angle can be equal to 1.45.

Therefore, we can conclude that no triangle exists with the given conditions.