Invested amount = $5,000.
Interest rate = 3.75% per year compounded quarterly, that is 4 times in a year.
First we would convert percentage into decimals 3.75%=3.75/100 = 0.0375.
Because interest is compounded quarterly, we need to divide 0.0375 by 4, we get 0.009375.
Number of years = 6 years.
n=4 (number of quarters in a year)
We can apply Compound interest formula.
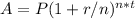 , Where P is invested amount, r is the rate of interest, it is the time in number of years and n is the number of installments.
, Where P is invested amount, r is the rate of interest, it is the time in number of years and n is the number of installments.
Plugging values of P, r, t and n in above formula, we get
A = 5,000 ( 1+
 )
)
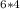
0.0375 divided by 4 gives 0.009375 and 6*4 = 24.
So, we could rewrite expression as,
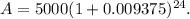
We can add 1+0.009375, we get 1.009375.
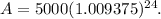
Expression could be written in any form
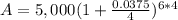 or
or
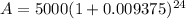 or
or
 .
.