Question

You plan on financing a new road bike for $2,500. The bike shop offers a 13.5% APR for a 24 month loan. Use this information, and the table above, to determine the monthly payments. Round your answer to the nearest cent.

Answer 1

This question can be approached using the present value of annuity formula. The present value of annuity is given by
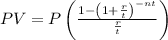
`PV=P\left( (1-\left(1+ (r)/(t) \right)^(-nt))/( (r)/(t) ) \right)`, where: PV is the present value/amount of the loan, P is the periodic (monthly in this case) payment, r is the APR, t is the number of payments in one year and n is the number of years.

Given that the financing is for a new road bike of $2,500 and that the bike shop offers a 13.5% APR for a 24 month loan.

Thus, PV = $2,500; r = 13.5% = 0.135; t = 12 payments (since payment is made monthly); n = 2 years (i.e. 24 months)

Thus,


`2500=P\left( (1-\left(1+ (0.135)/(12) \right)^(-2*12))/( (0.135)/(12) ) \right) \\ \\ =P\left( (1-\left(1+ 0.01125 \right)^(-24))/( 0.01125 ) \right)=P\left( (1-\left(1.01125 \right)^(-24))/( 0.01125 ) \right) \\ \\ =P\left( (1-0.764531)/( 0.01125 ) \right)=P\left( (0.235469)/( 0.01125 ) \right)=20.9306P \\ \\ \Rightarrow P= (2500)/(20.9306) =119.44`

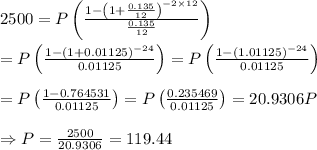
Therefore, his monthly payment is $119.44