Question

A park ranger is helping to restore the plant cover in a valley after a forest fire. He launches a cluster of seeds from a high point above the valley. The cluster's height above the valley floor can be modeled using the function given below.

h(t)= -4t^2+64t+320


How many seconds will it take for the seed cluster to reach the valley floor?


A.320 seconds

B.4 seconds

C.20 seconds

D.16 seconds

E.64 seconds

Answer 1

The cluster's height above the valley floor can be modeled by the equation:


`h(t)=-4 t^(2) +64t+320`

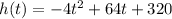
When the cluster seeds will reach the valley floor, the height of the cluster seeds above the valley floor will be 0. So substituting h(t) = 0 in the above equation we can find the time when the cluster seeds will reach the valley floor.


`h(t)=0=-4t^(2) +64t+320 \\ \\ -4t^(2) +64t+320=0 \\ \\ -4(t^(2)-16t-80)=0 \\ \\ t^(2)-16t-80=0 \\ \\ t^(2) -20t+4t-80=0 \\ \\ t(t-20)+4(t-20)=0 \\ \\ (t+4)(t-20)=0 \\ \\ t=-4,t=20`

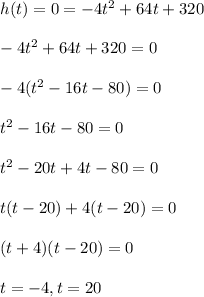
Since t represents the amount of time, it cannot have a negative value. So the only acceptable value of t is t=20

Thus it will take 20 seconds for the cluster of seeds to reach the valley floor. Thus the correct answer is option C