Question

Select the exclusion that fits best with this problem. 3x^2y^2-6xz/6x^2yz

Choices
x = 0
x, y, z = 0
1 + y + y^2, y = 0, 1 - y = 0
a, b = 0, a^2 + ab + b^2 = 0
2x - 1 = 0, 4x^2 + 2x + 1 = 0

Answer 1

Option B is correct .i.e., x , y , z = 0 must be excluded.

Explanation:

Given Expression:

`(3x^2y^2-6xz)/(6x^2yz)`

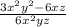
We have to find value of x , y and z which are to be excluded.

Value of variable of a expression are excluded for which expression does not exist.

Given expression is of fraction,

so, where denominator is going to be zero those value going to be excluded.

Here Denominator = 6x²yz

Denominator can not be equal to 0

So to find point where it become zero we put 6x²yz equal to 0

6x²yz = 0

⇒ x² = 0 or y = 0 or z = 0

Therefore, Option B is correct .i.e., x , y , z = 0 must be excluded.

Answer 2

For this case we have the following expression:
3x ^ 2y ^ 2-6xz / 6x ^ 2yz
From here, we must exclude all values that make the denominator equal to zero.
We have then:
6x ^ 2yz = 0
Therefore, the results are:
x = 0
y = 0
z = 0
Answer:
The exclusion that fits best with this problem is:
x, y, z = 0