Answer:
x=-3
Explanation:
The general equation of a parabola with vertex at the origin is
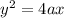
in the case that it opens horizontally and

in the case that it opens vertically. Moreover, in the case that the parabola opens horizontally, the point (0,a) is the focus of the parabola, and the directriz is the vertical line x=-a. The same is true but with interchanged coordinates for a parabola that open vertically.
In our case
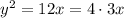
is a parabola that opens to the right with focus point (0,3) and vertical directriz
x=-3.