The given equation is the equation of the circle, as the coefficients of x² and y² have same values and same signs. This means the camera is located at the center of the circle.
The equation is in standard form, we can directly find the
center of the circle to be (9, -3) and the radius of the circle is 7.The car is parked at the location (-2, 5). Using the distance formula we can find the distance from camera to the car.
Using the distance formula we can write:
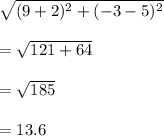 Thus the car is parked at a distance of 13.6 units from the location of the camera.
Thus the car is parked at a distance of 13.6 units from the location of the camera.