Remember that for a graphic of a trigonometric functions of the form
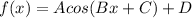

is the amplitude of the function
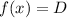
is the midline of the trigonometric function
We know form our problem that

, so the amplitude of our function is 5. We also know that the
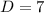
. So the midline of our function is the line
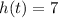
.
Using those two features we can conclude that the graph
that shows the height of the water at the dock at any time after midnight is: