Question

The graph of a transformed exponential function has the following characteristics:

horizontal asymptote at y = 3

passes through the points (1, 4) and (-2, 19)


What are the coordinates of the y-intercept?

A) (0, 49/16)

B) (0, 4)

C) (0, 7)

D) The graph does not cross the y-axis

Answer 1

C) (0, 7)

the value of the y-intercept must be greater than 4 and less than 19 based on the coordinates given. (0,7) is the only value that fits that range.

Answer 2

Explanation:

The graph of a transformed exponential function has to be found out

Since asymptote is y=3 we have

`y=ab^x+3`

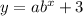
Substitute the given points to get

`4=ab+3\\19 = ab^(-2) +3\\16=(1)/(b^3) \\b=\sqrt[3]{(1)/(16) }`

Hence
`a=\sqrt[3]{16}`

The function would be

`y=\sqrt[3]{16}(\sqrt[3]{(1)/(16) })^x+3`

When x=0 y intercept = 5.52

Hence none of the choices matches this.