Question

How does changing the function from f(x) = −5 cos 2x to g(x) = −5 cos 2x − 3 affect the range of the function?

The function shifts down 3 units, so the range changes from −1 to 1 in f(x) to −4 to −2 in g(x).

The function shifts down 3 units, so the range changes from −5 to 5 in f(x) to −8 to 2 in g(x).

The function shifts down 5 units, so the range changes from −1 to 1 in f(x) to −6 to −4 in g(x).

The function shifts down 5 units, so the range changes from −5 to 5 in f(x) to −10 to 0 in g(x).

Answer 1

The correct option is 2.

Explanation:

The general form of a cosine function is

`y=A\cos (Bx+C)+D`

Where, a is amplitude,
`(2\pi)/(B)` is period, C is phase shift and D is midline or vertical shift.

The given functions are

`f(x)=-5\cos 2x`

`g(x)=-5\cos 2x-3`

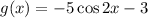
In f(x), D=0, it means midline is y=0. In g(x), D=-3, it means midline is y=-3. The graph of function f(x) shifts 3 units down to get the graph of g(x).

We know the the range of cosine function is [-1,1].

`-1\leq \cos 2x\leq 1`

Multiply both the sides by -5. If we multiply or divide the inequality, then the sides of inequality is changed.

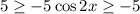`5\geq -5\cos 2x\geq -5` .... (1)

`5\geq f(x)\geq -5`

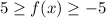
The range of f(x) is [-5,5].

Subtract 3 from each side of inequality (1).

`5-3\geq -5\cos 2x-3\geq -5-3`

`2\geq g(x)\geq -8`

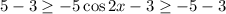
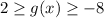
The range of g(x) is [-8,2].

The function shifts down 3 units, so the range changes from −5 to 5 in f(x) to −8 to 2 in g(x).

Therefore option 2 is correct.

Answer 2

For this case we have the following function:
f (x) = -5 cos 2x
The range of the function is given by:
[-5, 5]
We apply the following transformation:
Vertical translations:
Suppose that k> 0
To graph y = f (x) -k, move the graph of k units down.
We have then:
g (x) = -5 cos 2x - 3
Therefore, the range of the function changes to:
[-8, 2]
Answer:
The function shifts down 3 units, so the range changes from -5 to 5 in f (x) to -8 to 2 in g (x).