Question

What are the focus and the directrix of the graph of x=1/24 y^2

Answer 1

The given equation of parabola is:


`x= (1)/(24) y^(2)`

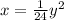Part 1) Focus of the Parabola

In order to find the focus and equation of directrix, we first have to convert the given equation to standard form of parabola.


`24x= y^(2) \\ \\ 4*6(x)= y^(2) \\ \\ (y-0)^(2) =4*6*(x-0)`

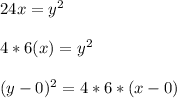
The focus of the general equation of parabola shown below lies at (h+p, k)

`(y-k)^(2)=4p(x-h)`

Comparing our equation to the general equation we get:
h=0
k=0
p=6

So the focus of given parabola will be (0+6, 0) = (6,0)

Part 2) Directix of the Parabola

The directrix of the general parabola shown above lies at:

x = h - p
Using the values of h and p, we get

x = 0 - 6

x = -6

So, the directrix of the given parabola has the equation x = -6