The correct questions is simplify the expression and write in standard form
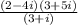
First we need to simplify the numerator of the fraction.
(2 - 4i)(3 + 5i) = 6 +10i - 12i -20i² = 6 - 2i + 20 = 26 - 2i
So the expression becomes:
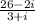
In order to remove the iota sign from denominator, we multiply and divide the fraction by its conjugate.
