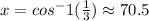Answer:
A numerical value of one trigonometric function of x, for the given function would be
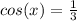
Explanation:
We know that there are many trigonometric functions, that can be expressed as functions of x, for example:
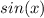
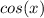
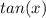

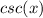
So, the problem is aking us for one trigonometric function of x, but gives us a product of functions of x, instead of one function of x. We note then, that

Therefore, we calculate from the given function
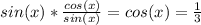
wich is our answer, furthermore, we could calculate the value of x for this case