Answer:
The graph in the attached figure
Explanation:
we have
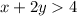
we know that
The solution of the inequality is the shaded area above the dashed line
The equation of the line is
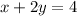
Find the x-intercept
For
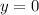

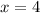
The x-intercept is the point
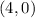
Find the y-intercept
For
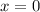
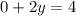
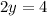
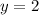
The y-intercept is the point
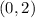
therefore
The graph in the attached figure