Question

Use a matrix to find the coordinates of the endpoints or vertices of the image of each figure under the given reflection.

quadrilateral HIJK with H(–5, 4), I(–1, –1), J(–3, –6), and K(–7, –3); y-axis

Answer 1

The vertices of the original quadrilateral can be written in matrix form using the vertex matrix. The vertex matrix is

`\begin{pmatrix}-5&-1&-3&-7\\ 4&-1&-6&-3\end{pmatrix}`

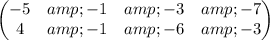
To find the coordinates of the endpoints or vertices of the image of the given coordinate points reflected about the y-axis, we just need to multiply the transformation matrix by the vertex matrix. The transformation matrix for this particular problem is

`\begin{pmatrix}-1&0\\ 0&1\end{pmatrix}`

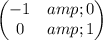
Multiplying the two matrices, we have

`\begin{pmatrix}-1&0\\ 0&1\end{pmatrix}\begin{pmatrix}-5&-1&-3&-7\\ 4&-1&-6&-3\end{pmatrix}=\begin{pmatrix}5&1&3&7\\ 4&-1&-6&-3\end{pmatrix}`

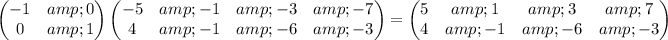
Therefore, the coordinates of the endpoints or vertices of the image are (5,4), (1,-1), (3, -6) and (7, -3).