Question

Scientists found an animal skull during an excavation and tested the amount of carbon-14 left in it. They found that 55 percent of the carbon-14 in the skull remained. How many years ago was the animal buried? Round your answer to nearest whole number. (Hint: A = A0e-0.000124t.)

A) 443,548 years
B) 362,903 years
C) 6,439 years
D) 4,821 years

Answer 1

55% of the Carbon is left in the skull.

If A₀ was the original amount of Carbon, the amount of Carbon that is remaining will be 55% of A₀ which equals 0.55A₀

Using the given equation:


`A= A_(o)e^(-0.000124t) \\ \\ 0.55A_(o)=A_(o)e^(-0.000124t) \\ \\ 0.55=e^(-0.000124t) \\ \\ ln(0.55)=ln(e^(-0.000124t)) \\ \\ ln(0.55)=-0.000124t*ln(e) \\ \\ ln(0.55)=-0.000124t \\ \\ t= (ln(0.55))/(-0.000124) \\ \\ t= 4821`

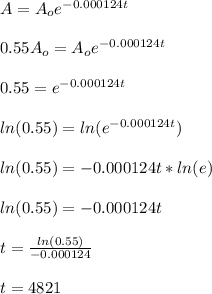Rounding of to nearest year, we can conclude that the animal was buried 4821 years ago. So option D gives the correct answer