Question

Cot^4θ-4cot^2θ-5=0 
solve for θ

Answer 1

`\cot^4\theta-4\cot^2\theta-5=(\cot^2\theta-5)(\cot^2\theta+1)=0`


`\cot^2\theta-5=0\implies\cot^2\theta=5\implies\cot\theta=\pm\sqrt5`

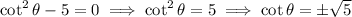
Recall that
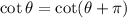
`\cot\theta=\cot(\theta+\pi)`, which is to say
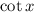
`\cot x` has period
`\pi`. This in turn means that
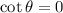
`\cot\theta=0` will have the same solutions as
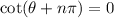
`\cot(\theta+n\pi)=0` for any integer
`n`. So the general solution to the first case is


`\cot\theta=\pm\sqrt5\implies\theta=\cot^(-1)(\pm\sqrt5)+n\pi`

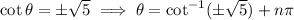
where
`n` is any integer.

On the other hand,


`\cot^2\theta+1=0\implies\cot^2\theta=-1`

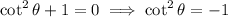
but
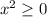
`x^2\ge0` for any value of
`x`, so this equation has no (real) solutions for
`\theta`.