The answer to your questions is that it depends on how we view the polynomial. In particular,

If the left hand side were factorizable, then we would be able to write it in the form
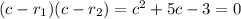
If we expand the leftmost expression, we'd get
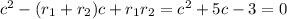
and so for the two polynomials to be the same, the coefficients must match. In other words, the unknowns
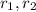
would have to satisfy
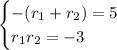
Suppose that, moreover, we want integer solutions for
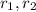
. For this to happen, they must be factor pairs of the constant term.
-3 only has two factor pairs. Either

and
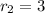
, or

and
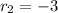
. In the first case, we'd get a linear coefficient of
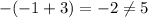
, while in the second, we'd get

.
There is no integer solution for this system, so the original quadratic is not factorizable - but only so over the integers.
If we change the scope of the coefficients, i.e. allow for any real numbers/complex numbers to appear in the factorization, then we always factorize a quadratic. The above system is easy to solve.
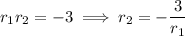
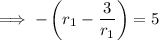
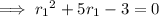
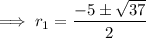

so the original quadratic is factorizable over the reals.