Question

What is the value of x in the triangle? Round your final answer to the nearest hundredth.

(Show your work.)

Answer 1

Answer: The required value of x is 19.42 units.

Step-by-step explanation: We are given to find the value of x from the figure.

We can see that

the figure contains a right-angled triangle with one acute angle of measurement 72°.

The lengths of the base and hypotenuse related to this acute angle are 6 units and x units respectively.

Therefore, from trigonometric laws of a right-angled triangle, we have

`\cos 72^\circ=(6)/(x)\\\\\Rightarrow 0.309=(6)/(x)\\\\\Rightarrow x=(6)/(0.309)\\\\\Rightarrow x=19.417.`

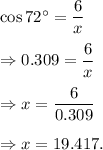
Rounding to nearest hundredth, we get

x = 19.42 units.

Thus, the required value of x is 19.42 units.

Answer 2

From SOH CAH TOA, you know that
cos(72°) = 6/x
x = 6/cos(72°) ≈ 6/0.309017

x ≈ 19.42